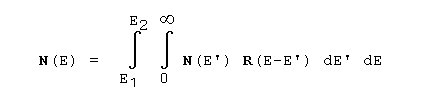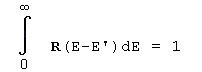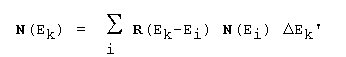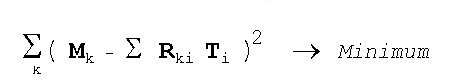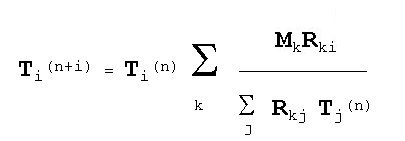Allgemeine Informationen zur Mikroanalyse
ESMA Info1
Info2
Info3
Info4
Info5
Info6
Info7
Info8
Mikro-RFA
Info1
Info2
Entfaltung überlagerter Linien
Auf Grund der Wechselwirkungsprozesse im Detektor und auf Grund des elektronischen Rauschens entstehen
Linienbreiten, die oft dazu führen, dass sich Linien verschiedener Elemente überlagern. Die Bestimmung der
Nettoimpulszahlen ist nicht mehr durch Kanalsummation möglich.
Es ist Aufgabe der Software durch ein mathematisches Verfahren aus dem Spektrengebirge, das sich aus verschiedenen Element -Linienserien additiv zusammensetzt, die einzelnen Spektrenanateile elementspezifisch wieder herauszuholen. Da die Verbreiterung der Linien durch das Spektrometer mathematisch mit einer "Faltung" beschrieben werden kann, heißt der umgekehrte Prozess "Entfaltung". Die Software muß also in vielen analytischen Fällen eine Spektrenentfaltung nutzen.
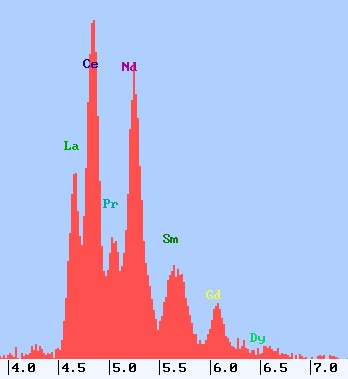
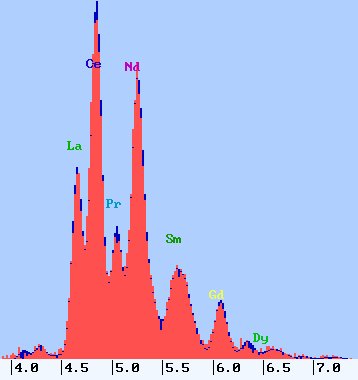Gemessenes Spektrum im Vergleich zum synthetischen Summenspektrum nach der Entfaltung ermittelt
(Spektrenrekonstrukton: blau)
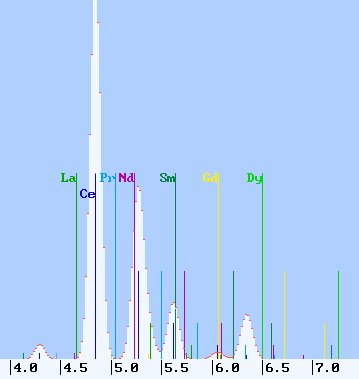
Am dramatischsten sind die Überlagerungen bei den L-Serien, da jedes Element viele Linien emittiert und benachbarte Elemente energetisch dicht beieinander liegen. Das Trauma jedes Röntgenspektrometers ist Monazit, das hier als Beispiel dienen soll.
Die Güte der Spektrenentfaltung kann man meist nur daran ablesen, wie das rekonstruierte Spektrum im Vergleich zum gemessenen aussieht. Manche Prozeduren liefern auch einen "Gütewert" der als Zahl Aussagen über die erreichte Approximation liefern soll.
Die Komplexität der Entfaltungsaufgabe lässt sich besser an der Überlagerung der einzelnen Linienserien (Bestandteile des gemessenen Spektrums) darstellen:
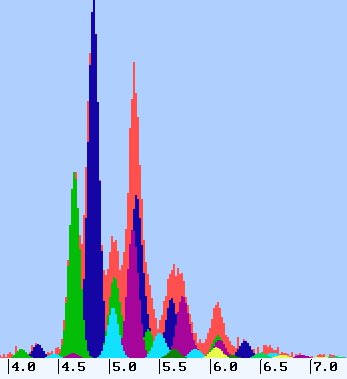Gemessenes Spektrum im Vergleich zu den jeweils in der Entfaltung ermittelten Einzelspektren
Zur Verdeutlichung der Entfaltungsproblematik zeigt das folgende Bild die Liniendichte und nur eine einzelne L-Linienserie des Elementes Ce im Vergleich:
Theorie:
Eine Umwandlung des Röntgenemissionsspektrums in
ein digitalisiertes Impulshöhenspektrum lässt sich unter Vernachlässigung der Spektrometereffektivität und des
emittierten Untergrundes (werden getrennt bei der Auswertung berücksichtigt) mit der Abbildungsfunktion R
beschreiben:
N(E')
Impulsverteilung der emittierten charakteristischen Strahlung
N(E)
gemessene Impulsrate im Energiebereich E1 bis E2
Es gilt:
Wenn man eine gemessene diskrete Impulsverteilung annimmt, ergibt sich:
Rki
Responsefunktion (Abbildungsfunktion, Faltung)
Mk
gemessene Impulsrate im Kanal k der festen Breite von 1 Kanal
Ti
emittierte Impulsrate des Elementes i
L
Zahl der Linienserien (Elemente)
Wenn die Zahl der betrachteten Kanäle gleich der Zahl der Elemente ist, so ist das Gleichungssystem nach den Ti
umstellbar und damit sofort zu lösen. Die Zahl der Unbekannten ist gleich der Zahl der Gleichungen. Als Kanäle
können auch die in der Identifizierung gewählten "Regions of interest" genommen werden (für jedes Element wird ein
Energiebereich gewählt). Wenn keine Überlappung existiert, so sind alle Rki = 1. Damit entsprechen die emittierten
Impulsraten genau denen im "Kanal" gemessenen. Wir haben die "triviale" Lösung des Gleichungssystems. Durch
Summation aller Impulszahlen im Energiebereich einer Linienserie erhält man die gesuchte, emittierte Impulszahl.
Bei leichten Überlagerungen sind die Rki nicht mehr identisch 1. Die Lösung des Gleichungssystems führt zur
sogenannten Überlappungskorrektur.
Bei komplexen Überlagerungen ist eine Lösung des Gleichungssystems durch die Vereinfachung K = L mit
Auswahl von Linienbereichen nicht mehr durchführbar. Es müssen alle Kanäle eines Spektrenbereiches, in dem sich
eine Linienüberlagerung befindet, herangezogen werden. Da die Zahl der Kanäle K > L ist, ist das Gleichungssystem
überbestimmt.
Das Entfaltungsmodell Fit:
Es wird ein Kriterium herangezogen, um das überbestimmte Gleichungssystem zu lösen. Zwischen Modell-
Linienserien und gemessenem Spektrum ist die Summe aller Quadrate der Abweichungen jedes Kanals zu minimieren.
Diese Methode ist eine lineare Parameteroptimierung und damit eigentlich keine echte Entfaltung. In der Literatur
werden häufig die Bezeichnungen "Fit", "Least Squares Fitting" oder "Methode der kleinsten Abweichungsquadrate"
verwendet.
Die Lösung führt zu einem linearen Gleichungssystem. Das Kriterium der Abweichungsquadratminimierung ist relativ willkürlich. Oft werden auch noch Wichtungsfaktoren eingeführt, um z.B. den Einfluß von kleinen
Kanalinhalten auf das Rechenergebnis zu minimieren (statistische Fehler !). Die Optimierung von nichtlinearen Parametern (Peaklagen oder Peakbreiten) führt zu einer nichtlinearen Parameteroptimierung, die iterativ gelöst wird.
Das Entfaltungsmodell Bayes:
Die Bayes- Entfaltung ist eine iterative Methode. Sie
ist eine echte Entfaltung und modelliert damit mathematisch die tatsächlichen statistischen Prozesse, die zur
Verbreiterung der Linien und damit zu Linienüberlagerungen führen.
Bei einer iterativ arbeitenden Methode sind Konvergenzschwierigkeiten nicht völlig ausschließbar. Eine Reihe von programmtechnischen Maßnahmen innerhalb der Iteration können das vermeiden.
Normalerweise ist der Analytiker zufrieden, wenn die Software eine Spektrenentfaltung beinhaltet und für ihn das Problem löst. Oft ist es aber nützlich, etwas über die als Black-Box arbeitenden Programme zu wissen:
Ein Nachteil der Bayes- Entfaltung gegenüber einer linearen Parameteroptmierung mit Fit ist die etwas größere
Anfälligkeit gegenüber Fehlern im Untergrundabzug. Das liegt darin begründet, dass eine Parameteroptimierung
entsprechend des Modellansatzes (Minimierung der Abweichungsquadrate zwischen Modell und Spektrum) immer
die hohen Impulszahlen bevorzugt, diese gegenüber von Untergrundapproximationsfehlern aber am unempfindlichsten
sind. Allerdings sollte eine möglichst exakte Untergrundapproximation so oder so eine Voraussetzung für die
Minimierung der Fehler sein.
Die Bayes- Entfaltung schneidet nach allen weiteren Kriterien besser als die Fit- Prozedur ab. Das liegt vor allem in
deren mathematischen Modellierung der tatsächlichen physikalischen Prozesse mit der Wahrscheinlichkeitstheorie.
Die mathematische Parameteroptimierung ist eher eine rein mathematische Methode und damit bei Modellfehlern in
ihrer Leistungsfähigkeit begrenzt. Fehler in der Energielage, der Koppelfaktoren der Linien einer Element -Linienserie
untereinander, Änderungen in der Auflösung des Spektrometers, Abweichungen von der Gaußform der Peaks
und sogar die Impulsstatistik haben einen wesentlich geringeren Einfluss auf das Entfaltungsergebnis einer Bayes-
Entfaltung im Vergleich zu Fit. Um so schwächer die Überlagerung ist, um so mehr vermindern sich auch noch die
verbleibenden Fehler und um so deutlicher tritt die Leistungsstärke der Bayes- Entfaltung hervor.
Bei tieferem Interesse mit weiteren Literaturangaben:
EGGERT, F.; SCHOLZ, W.
phys. stat. sol. (a) 97 (1986) K9
